Über die Polarographie
von Björn Schulz, Berlin 2003
Prinzip und Grundlagen der Polarographie
von Björn Schulz, Berlin 2003

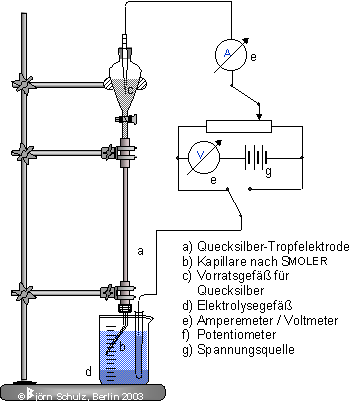
Das Kernstück der polarographischen Untersuchungen bildeten und bilden dabei die Quecksilberelektroden (Quecksilberstrahlelektroden, Quecksilberkapillarelektroden), z.B.
Der edle Charakter des Quecksilbers als geeignetes Elektrodenmaterial wegen der relativ hohen Wasserstoffüberspannung ist dabei schon früh bekannt gewesen, selbst seit Faradays Zeiten ist die vollständige Reinigung bekannt gewesen.
1873 untersuchte Lippmann die Veränderung der Oberflächenspannung von Quecksilber in Abhängigkeit vom angelegten Potential mit Hilfe der Veränderung des Meniskus in einer Kapillare als polarisierbare Elektrode, den Gegenpol bildete eine unpolarisierbare Quecksilberschicht als Elektrode 2. Art. Die Verschiebung des Meniskus war Indikator für die Änderung der Oberflächenspannung gemäß
2 π rK γ = π rK2 h s g
(rK - Kapillarradius; γ - Oberflächenspannung; h - Höhe d. Hg-Säule; s - spez. Gewicht v. Hg)
Praktische Anwendung dieses Prinzips findet sich im Kapillarelektrometer wieder.
Die Abhängigkeit der Oberflächenspannung zum Potential ist durch die Elektrokapillarparabel wiedergegeben.
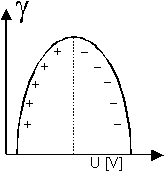
Abb. 01: Elektrokapillarparabel, Oberflächenspannung
aufgetragen gegen Potetial, mit Maximalwert
B. Kučera verwendete 1903 die Hg-Tropfelektrode, dabei wog er das Gewicht abfallender Tropfen und kam zu folgendem Zusammenhang:
mTropf t g = 2 π rK γ
(mTropf - Masse abfallender Hg-Tropfen; m - Hg-Menge, in der Polarographie üblicherweise als "Massenstrom" m bezeichnet, in [g/s]; t - Zeit, g - Erdfallbeschleunigungskonstante, andere v.s.)
Folgerung: m ¬ ~ paufKapillare, m ~ γ
Die dynamische Methode ist also eine Methode, bei der die Oberfläche der Hg-Elektrode in ständiger Bewegung ist.
Kučera beobachtete bei der Untersuchung von Elektrokapillarparabeln bei stark verdünnten Elektrolytlösungen sowie bei Lösungen niederer Fettsäuren einen anormalen Kurvenverlauf:
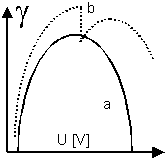
Abb. 02: a) normale Elektrokapillarparabel, b) anormaler Kuvenverlauf
Kučera beauftragte Jaroslav Heyrovský und Šimůnek 1918 mit der Untersuchung dieses Sachverhaltes. Zunächst kam es zu keiner Klärung, später erkannte man dieses Problem im Zusammenhang mit Turbulenzen des Elektrolyten an der Oberfläche der Elektrode.
Heyrovský befasste sich allerdings weiter mit der Hg-Elektrode, er verzichtete auf das Wiegen der Tropfen, und baute ein Spiegelgalvanometer, ein niederohmiges Potentiometer ein (10Ω - 20Ω).
Er veröffentlichte seine Ergebnisse, die Strom-Spannungskurven 1922 und von da an begannen die polarographischen Untersuchungen.

Jaroslav Heyrovský, Mit freundlicher Genehmigung:
Jitka Podzimkova, Internet Team - Radio Prague
Wichtige Daten zur Person
|
|
|
| 1922 | Prof. für PC in Prag |
| 1925 | Entwicklung der Polarographie |
| 1950 | polarographisches Institut in Prag |
| 10. Dezember 1959 | Nobelpreis für Chemie |
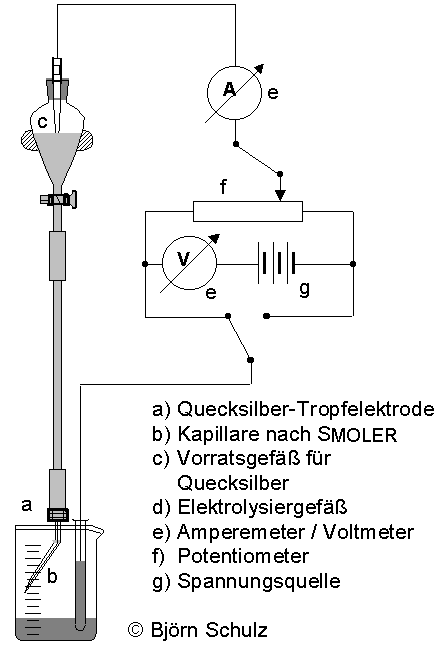
Abb. 03: klassische polarographische Messanordnung
Dabei ist auf die Entfernung von Sauerstoff in der Probelösung zu achten, eine inerte Atmosphäre gewährleistet werden. (Novák, Kalousek, Šerák).
Der Radius rK beträgt in der Regel 0,05 - 0,08 mm, die Behälterhöhe bedingt die Tropfzeit, die etwa zwischen 2 - 4 s liegt.
Der Strom wurde ursprünglich mit einem gedämpften Spiegelgalvanometer, heute allerdings mit speziellen elektrischen Messschaltungen erfasst.
Ist die elektromotorische Kraft Null (EMK = 0), dann liegt ein Kurzschluss vor.
Der Einfluss des Potentiometerwiderstandes ist für die Genauigkeit der Messung maßgebend, er muss möglichst klein sein.
| I = |
|
Þ I = |
|
|
|
|
p = EV − I R
Bei Anwesenheit eines indifferenten (nicht an elektrochem. Prozessen beteiligten) Grundelektrolyten und einem Strom I = 10−5 A ergibt sich:
p = EV Þ EK = − EV + EA ~ − EV, da
− EV = const., die Gegenelektrode ist unpolarisierbar, nur die Hg-Elektrode bedingt die Polarisation.
Also gilt bei Potentialkurven: EK ~ − EV, I ~ E.
Bei anderen Bezugselektroden, als z.B. reines Bodenquecksilber, führt zu identischen Kurvenverläufen, die verschoben sind in Richtung der Potentialdifferenz.
Das heißt: Die Gestalt der Strom-Potential-Kurven hängt nicht vom Potential der Bezugselektrode ab, sondern vom Potential der polarisierten Tropfelektrode (und dieses von der Beschaffenheit der Elektrolytlösung).
Wichtige Merkmale:
Als Messergebnis steht am Ende einer polarographischen Analyse das Polarogramm. Es kann unterschiedlich je nach Wahl der polarographischen Methode beschaffen sein, trägt jedoch stets die selben chemischen Informationen, die dem Analytiker von Bedeutung sind. Polarogramme sind im Allgemeinen Kurven, bei denen einem angelegten Potential (bzw. Spannung) auf der Abzisse eine Stromstärke auf der Ordinate zugeordnet sind. Ganz klassisch ergeben sich Zickzackkurven bei Messungen mit der DME, bei modernen Verfahren wird die Kurve mit Hilfe eines Rechners (früher mit speziellen kompliziertern Schaltungen) aufgearbeitet, mit Hilfe eines Integrators oder eines Rechners kann man die Kurve in die Form dI/dU = I' überühren, um eine zeitgemäße Analyse abgeben zu können.
Ein Beispiel für ein (klassisches) Polarogramm könnte so aussehen:
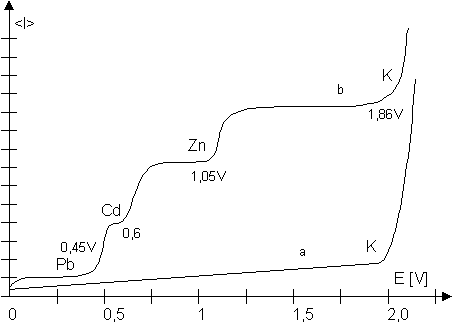
Abb. 04: Polarogramm mit vielen polarographischen Stufen
(sog. polarographisches Spektrum)
Bis 1,8 V Polarisationsstrom (sog. Kapazitätsstrom: Elektrode lädt sich auf, wie ein Kondensator)
Ist P ≥ 1,8 V, erfolgt eine Verminderung um I R:
P = EV − I R
Die Polarisation wird dann bei jedem Prozess an der DME vermindert, wenn dieser mit einer Elektronenübertragung (Stromdurchgang) verbunden ist, i.e.
Depolarisationsvorgänge werden durch anwesende Stoffe, die reduziert (geben Elektronen ab: Kathode) oder oxidiert (nehmen Elektronen auf: Anode; merke stets "anodische Oxidation") werden, hervorgerufen, in der Polarographie werden diese daher Depolarisatoren genannt.
| Es gilt: | P = EAnode − EKathode P = EV − I R | Þ | EK = − EV + EA EA:= 0 EK = − EV |
Aus EK = − EV ist ersichtlich, dass die angelegte äußere Spannung durch das Potential an der Kathode (hier: DME) bestimmt wird, das Potential der Anode ist je nach Bezugssystem maßgeblich, kann daher als konstant angesehen werden, was für den Kurvenverlauf nicht von Bedeutung ist, man kann daher EA:= 0 definieren.
Falls EK > 1,8 V ist, wird eine Abscheidung von Kalium-Ionen hervorgerufen, anders ausgedrückt:
K+-Ionen verhindern, dass die Polarisation über 1,8 V liegt.
Neben Kaliumionen werden hier andere Ionen abgeschieden. Man kann diese an den "Stufen" in dem Polarogramm erkennen.
Es baut sich ein Kapazitätsstrom auf, bis das erste Abscheidungspotential erreicht wird etc.
An der DME laufen dabei nacheinander folgende Reaktionen ab:
Pb2+ + 2e− → Pb
Cd2+ + 2e− → Cd
Zn2+ + 2e− → Zn
K+ + e− → K
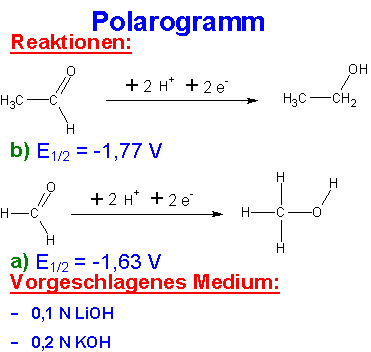
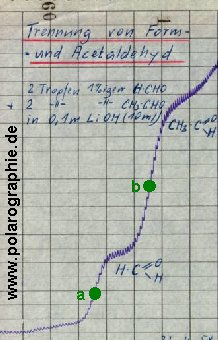
Ein Polarogramm organischer Substanzen sieht dann so aus, die entsprechenden Reaktionen sind angegeben:
|
|
Abb. 05: Polarogramm zweier organischer Substanzen
Der Prozess an der Kathode (Men+ + n e− → Me) bewirkt eine chemische Polarisation des Hg-Tropfens, weil reines Hg in verdünntes Quecksilberamalgam überführt wird.
Es gilt die Gleichung von Nernst:
| EK = − |
|
ln |
|
|
|
|
cMen+ - Konzentration in der Elektrolytlösung = Konzentration an der Elektrodenoberfläche; R - allg. Gaskonstante; T - absolute Temperatur in K, k - Konstante, charakterisiert durch elektrolyt. Lösungsdruck v. Me.
Die Konzentration an Me, welches amalgamiert wird, ist proportional von I, also die elektrolytisch abgeschiedene Stoffmenge ist proportional zum Stromdurchgang:
cMe = k* I, cMe ~ I
| − EV = EK = − |
|
ln |
|
Þ <I> = |
|
exp − |
|
|
|
|
|
|
<I> ist abhängig vom Potential an der DME
|
|
= |
|
|
exp − |
|
|
|
|
|
|
|
Steigung dI/dE ist abhängig von n (Wertigkeit der Ionen)
Polarographische Messungen werden in der Regel mit speziellen Messsystemen, die alle wichtigen Komponenten integrieren, durchgeführt. Diese speziellen Messsysteme werden Polarographen genannt.
Der erste Polarograph wurde von Jaroslav Heyrovský und dem Japaner Masuzo Shikata 1925 betrieben. Er bestand zunächst aus einer Messzelle mit DME, der Strom wurde über ein Spiegelgalvanometer, welches eine über eine von einem Motor getriebene Photokassette, registriert, geregelt wurde das ganze von einer Kohlrauschtrommel.
Die DME, dropping mercury electrode, besteht aus einer Kapillare, aus der das Quecksilber Tropfenweise heraustropft, sowie einem Quecksilberbehälter. Diese sind über einen Schlauch mit einander verbunden.
Die Ausflussgeschwindigkeit m ist durch das Gesetz von Hagen-Poiseulle zugänglich:
| m = |
|
= k p |
|
|
(π - Ludolfsche Zahl, PI; s - spez. Gew. Hg.; η - Viskositätskoeff. v. Hg; L - Länge Kapillare; P - effektiver hydrostat. Druck)
PC = hC g s; PR = 2η r−1
V(Tropfen) = m t s−1 = 4/3 p r3
| r = | ( | 3 m t | ) | 1/3 |
|
|
Für die Tropfzeit von einem Tropfen gilt:
t1 = k 1/h; t1 ~ 1/h
Die Tropfzeit ist antiproportional zur Behälterhöhe.
Oberfläche A des Quecksilbertropfens:
A(Hg) = 4 π r2
| A = 4 π r2 = |
|
= 0,85 m2/3 t2/3 |
Mittlere Oberfläche der Hg-Elektrode
| <A> = | 1 | ∫ | t1 | 0,85 m2/3 t2/3 dt = 3/5 0,85 m2/3 t2/3 = 0,51 m2/3 t2/3 | |
|
|
0 |
mechanische Regulierung der Tropfzeit:
Es gilt: m t = const.
1948 wurde durch mechanisches abreißen des Tropfens erreicht, dass Ausflussgeschwindigkeit und Tropfzeit unabhängig variiert werden konnten.
m ~ Behälterhöhe h
Experimentell ist die Regulierung mit Hilfe verschiedener Methoden möglich:
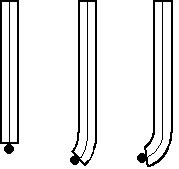
Abb. 06: Formen von Kapillarelektroden
t(ma) ≥ t(mb) ≥ t(mc)
Quecksilberstrahlelektroden dienen in der Polarographie und in der oszillographischen Polarographie, die hohe Ausflussgeschwindigkeit bewirkt u.U. f. d. Polarographie sehr hohe Ströme (I ≥ 10−3 A). Wegen der hohen Polarisierung werden andere, spezielle Bezugselektroden erforderlich. Oberflächenprozesse bewirken ein Mitreißen der elektrochemischen Doppelschicht, was besondere Auswirkungen auf die Prozesse an der Oberfläche der Elektrode haben kann (v.s.).
Es gilt:
| IKap. = IC = |
|
= E* |
|
|
|
|
C = C A(Hg), A(Hg) = 0,85 m2/3 t−1/3
IC = E* C dA(Hg)/dt = E* C 3/2 0,85 m2/3 t−1/3
Þ<IC> ~ h
Auch die Art der Doppelschicht beeinflusst, wie e.g. Pyridin in pH = 7.
In der Praxis ist IC unerwünscht, da sie der polarographischen Empfindlichkeit eine Grenze setzt. Ist nDepolarisator < 10−5, dann wird die polarographische Stufe so klein, dass sie durch IC überlagert werden kann.
| C' = |
|
, E* = E − Em |
|
|
Für die differentielle Kapazität gilt:
| Cd = |
|
= |
|
= C' + E* |
|
|
|
|
|
Für die integrale Kapazität ergibt sich:
| C' = |
|
∫ | Cd dE* | |
|
|
Cd ändert sich besonders stark bei der Adsorption grenzflächenaktiver Stoffe. Cd ist experimentell zugänglich über die Messung mit einer Wienscher Impedanzbrücke.
Dabei sind folgende Punkte zu beachten:
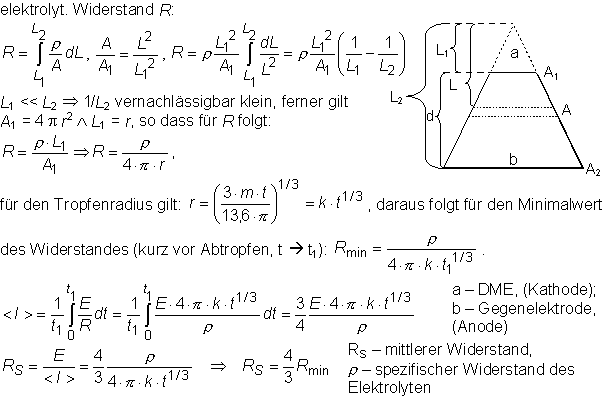
V. 1. Der Einfluss von cZusatzelektrolyt
Bei jeder polarographischen Stufe wird ein spannungsunabhängiger Strom, ein Grenzstrom erreicht.
Man unterscheidet dabei:
Durch einen Überschuss an Zusatzelektrolyten (um das 50 - 100fache relativ zur Depolarisatorkonzentration) wird der Wanderungsstrom IM = 0 und der Grenzstrom allein durch Diffusion bedingt.
Da die Diffusion eine stoffspezifische Eigenschaft ist, ist dies natürlich besonders wichtig für die analytische Aussagefähigkeit.
Heyrovský unterscheidet 4 Fälle von Grenzströmen:
DME sei die Kathode
Es gilt: <IL> = <Id> + <IM>
<IL> - mittlerer Grenzstrom; <Id> - mittlerer Diffusionsstrom; <IM> - mittlerer Migrationsstrom
Durch Zugabe eines (indifferenten) Grundelektrolyten kann der Grenzstrom bei der Reduktion erheblich gesenkt werden.
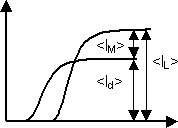
Abb. 07: Diffusionsstrom <Id> und Grenzstrom <IL> der
Kationen bei kathodischer Reduktion
Kathodisch. Der Wanderungsstrom fließt der Diffusionsrichtung entgegen:
<IL> = <Id> − <IM>
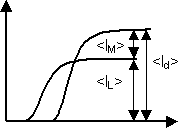
Abb. 08: Diffusionsstrom <Id> und Grenzstrom <IL> der
Anionen bei kathodischer Reduktion
<IL> = <Id> − <IM>, v.s.
Die Quecksilberelektrode als Anode, kann durch Anionen depolarisiert werden, e.g.:
Fe(CN)64− → Fe(CN)63− + e3−
Hg22− + 2 Cl− → Hg2Cl2
Dabei treten keine Wanderungsströme auf: <IM> = 0.
Der Grenzstrom ist allein diffusionsbedingt: <IL> = <Id>.
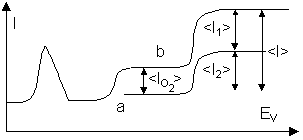
Abb. 09: Schema der Exaltation des Wanderungsstromes eines Kations,
Kurve(a): verd. NaCl-Lösung (rein), Kurve(b): verd. NaCl-Lösung, an der Luft gestanden
Es gilt dabei folgender Zusammenhang: <IO2> − <I2> = <I>, <Iexalt.> = <I2> − <I1>.
Die Exaltation ist unabhängig von der Depolarisatorkonzentration, sie ist jedoch ein charakteristisches Merkmal für die Qualität des Analyten bzw. Depolarisators.
VI. 1. Allgem. Ansatz gem. Faradaysches Gesetz
| I = n F |
|
|
|
dN/dt - Zahl an Depolarisatormolen pro Zeiteinheit, welche an der Elektrode elektrochemisch umgesetzt werden; F - Ladungsmenge in Faraday (ca. 96500 Coulomb), n - Zahl an e−
Þ Diffusion! Þ dN/dt kann durch das Ficksche Gesetz berechnet werden, die Stärke des Diffusionsstromes ist zugänglich.
Die Diffusion ist ein spontaner Prozess, sie ist bestrebt, einen Konzentrationsunterschied auszugleichen. Der Konzentrationsunterschied bewirkt einen Stofffluss von choch → cniedrig.
vDiffusion ~ Konzentrationsgradient, ~ Eigenschaften diffundierender Teilchen.
Die lineare Diffusion besagt, dass die Diffusion nur in eine Richtung verläuft.
| dN = D A |
|
dt |
|
|
Der Konzentrationsgradient a.d. Elektrodenoberfläche ist durch einen partiellen Differentialquotienten gegeben:
| ( |
|
) | |
|
|
x = 0 |
| I = n F |
|
= n F A D = | ( |
|
) | |
|
|
|
x = 0 |
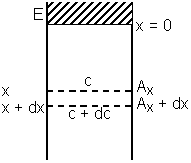
Abb. 10: Schematische Darstellung zur linearen Diffusion.
Es werden dabei folgende Zusammenhänge herangezogen:
|
|
= D |
|
|
|
|
| ( |
|
) | = | c − c0 | |
|
|
x = 0 |
|
| I = n F A D | c − c0 |
|
|
Þ Konzentrationsgradient a.d. starren, kugelförmigen Elektrode durch 2. Ficksches Gesetz zugänglich:
Folgende Gesetzmäßigkeiten liegen dabei der sphärischen Diffusion zugrunde:
|
|
= D [ |
|
+ | 2 |
|
] | |
|
|
|
|
|
| ( |
|
) | = C ( |
|
+ |
|
) | |
|
|
r = r0; t |
|
(π D t)1/2 |
| I = n F A D c ( |
|
+ |
|
) |
|
|
(π D t)1/2 |
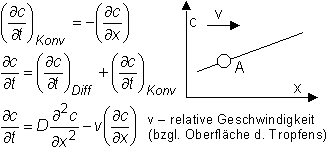
Abb. 11: Konzentrationsverteilung in der Nähe der Elektrode.
Die Ermittlung von V kann aus der Betrachtung von zwei konzentrischen Kugeln erfolgen, wobei ra bis zur Oberfläche des Hg-Tropfens reicht und rb fiktiv angenommen wird, ΔV = const., weil also praktisch nicht komprimierbar.
Für eine Änderung von ΔV ergibt sich: ΔV = V2 − V1 = 4/3 π (r23 − r13)
r2 − r1 := x = = Þ r2 = x + r1
ΔV = V2 − V1 = 4/3 π [(r1)3 − r13) ≈ 4 π r12 x = A x = const.
| A |
|
+ x |
|
= 0 |
|
|
|
| v := |
|
= − |
|
|
|
|
|
|
|
v = − 2/3 x t−1
Dabei beschreibt folgende Gleichung den Stofftransport zur linear wachsenden Elektrode:
| ∂c | = D | ∂2c | + | 2 | x | ∂c | ||
|
|
|
|
|
|
Diese Formel beschreibt den Stofftransport zur linear wachsenden Elektrode.
Betrachten wir die Anfangsbedingungen:
Ferner gelten folgende Zusammenhänge:
| ( |
|
) | = | c − c0 | |
|
|
x = 0 |
|
| I = n F |
|
= n F A D = | ( |
|
) | |
|
|
| x = 0 |
geht über in
| I = n F A D | c − c0 |
|
|
| I = n F A D | c − c0 |
|
|
ID = 0,732 n F (c* − c0)D1/2 m2/3 t1/6.
Die Konzentration c0 ist potentialabhängig.
Bei negativeren Potentialen einer Reduktionsstufe und genügend positiven einer Oxidationsstufe verarmt der Depolarisator an der Elektrode: C0 Û 0.
ID = 0,732 n F c D1/2 m2/3 t1/6.
Für Diffusionsbedingte Ströme gibt es eine charakteristische Zeitabhängigkeit der Ströme.
Nach k t1/6 ist ein parabolischer Anstieg auf einen Maximalwert kurz vorm Abtropfen des Quecksilbertropfens zu konstatieren.
Die Stromstärke sinkt zwar nach I = k t−1/2, die Oberfläche des Tropfens wächst jedoch schneller (vgl. Graphik), denn A ~ t2/3.
Dieses erklärt die parabolische Zeitabhängigkeit von der Stromstärke I an einer tropfenden Elektrode, wie es bei der DME der Fall ist, und damit wird im Polarogramm entsprechend ein Zick-Zack-Verlauf enthalten sein.
Die charakteristischen Zecken hängen also mit der Tropfzeit und der damit veränderten Oberfläche der Tropfelektrode zusammen. Beeinflussen kann man diese Darstellung auf dem Polarogramm mit der Einstellung der Empfindlichkeit des entsprechend verwendeten Galvanometers.
Für die mittlere Stromstärke gilt:
| <I> = | 1 | ∫ | t1 | I dt | |
|
|
0 |
Gleichung für den mittleren Diffusionsstrom, eigentliche Ilkovič-Gleichung:
<I>D = 0,627 n F (c − c0) D1/2 m2/3 t1/6, ist c0 = 0, gilt:
<I>D = 0,627 n F c D1/2 m2/3 t1/6
Wird F in die numerische Konstante gezogen (oftmals auch so in der Literatur auffindbar) ergibt sich <I>D zu:
<I>D = 607 n c D1/2 m2/3 t1/6.
Andere Schreibweisen (bes. angelsächsische Literatur) beziehen sich auf den Momentanstrom ID:
ID = 706 n c D1/2 m2/3 t1/6,
auch hier wird F in die numerische Konstante einbezogen.
Gültigkeit und Einschränkungen f. d. Ilkovič-Gleichung:
Man sollte im Allgemeinen bei einer polarographischen Messung die Temperatur angeben, zu Temperaturabhängigkeit kommen wir später.
Es gilt folgende Formel für die integrale Dicke der Diffusionsschicht (nach von Stackelberg).
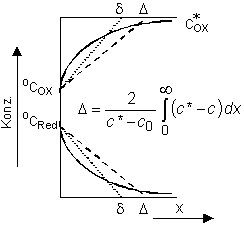
Abb. 12: Konzentrationsverteilung in der Diffusionsschicht,
obere ausgezogene Kurve: oxidierte Form, untere: reduzierte Form.
Gegeben seien m, t1 durch das Verwenden der gleichen Kapillare bei gleicher Höhe der Quecksilbersäule.
<I>D = <χ> c, mit dem sog. Ilkovič-Faktor:
<χ> = 0,627 n F D1/2 m2/3 t1/6.
| Es gilt jeweils für die | |||||||
|
Ausflussgeschwindigkeit m: m = k h |
Tropfzeit t1 t1 = K h-1 |
||||||
| daraus folgt: | |||||||
|
|||||||
|
Der mittlere Diffusionsstrom ist proportional zu h1/2 <ID> ~ h1/2 |
|||||||
Bei einer analytischen Bestimmung muss man daher auf eine bestimmte Behälterhöhe geachtet werden und die gleiche Kapillare beibehalten werden. Man kann über diese Eigenschaft indirekt bestimmen, ob ein Diffusionsstrom zugrunde liegt.
Bei der Verwendung verschiedener Kapillaren ist die Angabe von m (Massenstrom) und t1 (Tropfzeit für einen Tropfen) erforderlich. Es genügt folgende Verhältnisgleichung:
| ID1 | = | m12/3 (t1)11/6 |
| ID2 | m22/3 (t1)21/6 |
Ferner existiert eine potentialbedingte Tropfzeitänderung.
Starke Unterschiede in den Potentialwerten führt durch eine Änderung der Quecksilberoberflächenspannung zu einer Änderung der Tropfzeit, wie ID steigt bzw. sinkt, ist an der Elektrokapillarparabel ersichtlich. Die Änderung von ID ist nur geringfügig, denn t1 geht in <ID> = k t11/6 mit der sechsten Wurzel ein.
Bild: Elektrokapillarparabel Das Potential E muss für den Fall berücksichtigt werden, wenn zwei Stoffe in gleicher Konzentration c, aber erheblich auseinanderliegenden Depolarisatorpotentialen vorliegen.
Es gilt:
| 1 | dID | = | 1 | dD | + | 2 | dm | + | 1 | dt1 | ||||
|
|
|
|
|
|
|
|
|
Man kann diese Gleichung mit Koeffizienten vereinfachen: Aus
| ω =: | 1 | dID | α =: | 1 | dD | β =: | 1 | dm | σ =: | 1 | dt1 | ||||
|
|
|
|
|
|
|
|
|
wird: ω = 1/2 α + 2/3 β + 1/6 σ
Ferner gilt folgender Zusammenhang:
| α = | 1 | + | 1 | dΛ∞ | |
|
|
|
|
Es gilt folgender Zusammenhang zwischen Diffusionskoeffizient und Temperatur:
| D = | R T | Λ∞ |
|
|
Für die meisten Ionen gilt: 2,78% ≤ α ≤ 2,99%, für H+: α = 1,88%.
| m ~ | 1 | m = | 6 | Þ β = | 1 | dm | = − | 1 | dη | = −ε | ||
|
|
|
|
|
|
|
m(Tropfen) = m t1 g = 2 π r γ = α' γ
(m: Ausflussgeschwindigkeit, "Massenstrom"; m(Tropfen): Masse des Hg-Tropfens; γ - Oberflächenspannung Hg)
| t1 = | α γ | = | α γ η |
|
|
|
| δ = |
|
d(α γ η /6) | = | 1 | dη | + | 1 | dγ | = ε + φ | |||
| α γ η |
|
|
|
|
|
| ω = | 1 | (α − ε) | 1 | + φ |
|
|
|
ε = − 0,48% (ε - Temperaturkoeffizient der Viskosität des Quecksilbers)
| 1 | φ << α, δ |
|
|
| ω = | 1 | (α + 0,48) % |
|
|
Für die meisten Ionen gilt: ω ≈ 1,7%, für H+ ≈ 1,18%.
Bestimmung von α:
| α = | 1 | + | 1 | dΛ∞ | = | 1 | + ν | |
|
|
|
|
|
Waldensche Beziehung: Λ∞ η' = konst.
| Λ∞ | dη' | + dη' | dΛ∞ | = 0 |
|
|
|
| ν = |
|
− | dΛ∞ | = − | 1 | dη' | = 2,43% | |
|
|
|
|
|
α(21C) = 2,77%
| ω = | 1 | (2,77 + 0,48) % = 1,63% |
|
|
Dieser Wert ist mit dem experimentell bestimmten Temperaturkoeffizient von Nejedlý im Bereich [20 - 50C] im Durchschnitt mit 1,63%/1C vergleichbar.
Facit: Trotz des niedrigen Temperaturkoeffizienten muss bei quantitativen Bestimmungen die Temperatur auf ± 0,5C konstant gehalten werden, damit der Fehler bei der Ermittlung von <ID> 1% nicht übersteigt.
<ID> ~ c bei ± 1%,
<ID> ~ m2/3 t11/6 bei ± 3%,
und
| I := |
|
0,627 n F D1/2 bei ± 5%. |
| c m2/3 t11/6 |
Daher wurde Gleichung entwickelt, die diese begrenzten Genauigkeiten vermindern sollte.
Die Herleitung der Ilkovič-Gleichung vernachlässigte die Krümmung der Elektrode und sah nur eine lineare Diffusion vor. Aus der Ilkovič-Gleichung der linearen Diffusion zur stationären Elektrode konnte jedoch eine Gleichung hergeleitet werden, die die Verringerung der Diffusionsschicht an der wachsenden Elektrode mit Hilfe des Korrekturfaktors (7/3)1/2 berücksichtigte. Auch aus der Gleichung für die sphärische Diffusion zur wachsenden kugelförmigen Elektrode kann analog vorgegangen werden.
| I = n F A D c ( |
|
+ |
|
) |
|
|
(π D t)1/2 |
geht über in:
| <I>D = 0,627 n F c D1/2 m2/3 t11/6 | ( | 1+ 3,9 | D1/2 t11/6 | ) |
|
|
Koutecký arbeitete eine exakte Ableitung aus:
ID = 0,732 n F c m z (1 + 3,9z + 1,5z2)
<I>D = 0,627 n F c m z1 (1 + 3,9z1 + 1,5z12)
mit:
| z = | D1/2 t1/6 |
|
|
| z1 = | D1/2 t11/6 |
|
|
Es gilt hierbei:
| <I>D = 0,627 n F c D1/2 m2/3 t11/6 | ( | 1 − | A D1/2 t11/6 | ) |
|
|
Mit der Äquivalentleitfähigkeit, einer zentralen elektrochemischen Größe, Λ∞, also bei unendlicher (fiktiv) Verdünnung ergeben sich die folgenden Zusammenhänge:
| D∞ = | R T | Λ∞ (Nernst) |
|
|
| D∞(25C) = | 2,67 10−7 Λ∞ |
|
|
D∞ ~ T
...
Indirekte Methode zur Bestimmung von D (nach Rulf)
...
Man geht bei dieser Bestimmungsmethode wie folgt vor. In einer Messanordnung, welche einen Stoff erfasst, der durch eine Fritte (Pore durchteilt zwei gleichgroße Räe) diffundiert. Nach Zeitintervallen wird zeitabhängig die Konzentration ct. Siehe Bild.
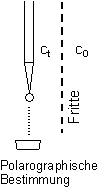
Abb. 13: Schema der Bestimmung von D
(nach Rulf über Referenzsubstanz, Dbekannt)
Es gilt dabei folgender Zusammenhang:
K D t = lg c0 − lg (c0 − 2ct)
K - Gerätekonstante, wird dann über ein bekanntes D ermittelt.
| D = | K |
|
|
<ID> (η)1/2
Es tritt bei Komplexierung eine Änderung des Solvatationsverhaltens ein (größere Moleküle), diese bedingte einen Einfluss auf die Diffusionskonstante D und damit auf die polarographische Bestimmung,
Als grundlegende Gleichung dient auch hier eine besonders wichtige Beziehung der Elektrochemie, die Nernstsche Gleichung, seltener wird sie auch als Peterssche Gleichung angegeben.
| E = E0 − |
|
ln |
|
|
|
|
Diese Gleichung setzt ein reversibles thermodynamisches Gleichgewicht vorraus, das gilt eigentlich für den stromlosen Zustand. Daher muss eine notwendige Bedigung bei einer Durchtrittsreaktion (Oxidation oder Reduktion) gelten: zum einen Reversibilität der Durchtrittsreaktion, zum anderen muss sie mit großer Geschwindigkeit ablaufen. Es muss ein mobiles Gleichgewicht zwischen oxidierter und reduzierter Form vorliegen.
Ilkovič: <I> = <χ> (cOx − cOx0)
<χ> = 0,627 n F D1/2 m2/3 t11/6
Kontinuitätsgleichung: <I> = <χ>' (cRed0 − cRed)
<χ>' = 0,627 n F D'1/2 m2/3 t11/6
Da nur die oxidierte Form des Depolarisators vorliegt, gilt: cRed = 0.
<I> = <χ> cRed0
| E = E0 − |
|
ln |
|
<χ> | |
|
|
<χ> cOx − I |
|
<χ> cOx = <ID>
| E = E0 − |
|
ln |
|
(D / D')1/2 mit (D / D')1/2 ≈ 1 | |
|
|
<ID> − <I> |
| <I> = |
|
|
|
| E1/2 = E0 − |
|
ln |
|
|
|
Das ergibt: E1/2 = E0.
Man kann daher einige wichtige Fakten schlussfolgern. Das Halbstufenpotential ist unabhängig von der Depolarisatorkonzentration, den ganzen gerätespezifischen Konstanten, es ist daher eine stoffcharakteristische Größe, die eine qualitative Aussage darstellt (Art des Depolarisators)
Das Halbstufenpotential ist gleich dem Standardpotential, falls der Depolarisator nicht mit dem Quecksilber amalgamiert. Amalgamiert es doch, dann entspricht es dem Standardpotential der entsprechenden Amalgamelektrode.
...
Liegen ein reduzierendes sowie ein oxidierendes System vor, dann gilt:
...
Sind mehrere Depolarisatoren in Lösung vorhanden, deren Standardpotentiale weit genug auseinanderliegen, erhält man mehrere polarographische Stufen. Es gilt das Prinzip der Additivität der Diffusionsstromstärken (Gesamtstromstärke).
Dabei entspricht die polarographische Kurve der potentiometrischen Titrationskurve, falls auf der Stromstärkenachse die Menge des Titriermittels aufgetragen wird.
Bei potentiometrischen Titrationen wird dem zu titrierenden Stoff durch das Titrationsmittel Elektronen (e−) übertragen,
bei polarographischen Verfahren erfolgt dagegen die Elektronenübertragung nur in der Elektrodenumgebung (daher auch die Bezeichnung "Titration durch Elektronen").
Das Standardredoxpotential, welches bei der potentiometrischen Titration 50% des Titriermitteläquivalentes entspricht, ist praktisch mit dem polarographischen Halbstufenpotential identisch.